Για να κερδίσει κανείς μια επίσημη παρτίδα στο σκάκι υπάρχουν πέντε και μόνο τρόποι:
- Κάνει ματ στον αντίπαλο
- Εγκαταλείπει ο αντίπαλος
- Μηδενίζεται ο χρόνος στο ρολόι του αντιπάλου ή όπως λέγεται στη σκακιστική ορολογία πέφτει η σημαία του
- Σε κάποιες ειδικές περιπτώσεις παράβασης κάποιου κανόνα μεσολαβεί ο διαιτητής και κατακυρώνει τη νίκη, π.χ., αντικανονική κίνηση αντιπάλου, κτλ.
- Σε κάποιες εξαιρετικές περιπτώσεις συμπαντικής φύσεως, π.χ., παύουν να ισχύουν οι νόμοι της φύσης, καταρρέει το σύστημα λογικής, κτλ.
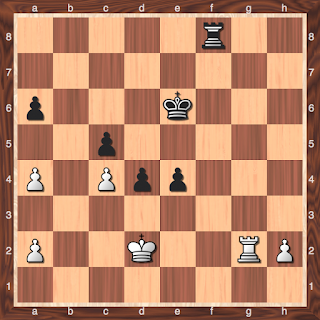
Θύμα αυτού του διλήμματος έχω πέσει κι εγώ. Η επόμενη θέση προέρχεται από μια επίσημη διαβαθμισμένη παρτίδα μου στο ομαδικό πρωτάθλημα Θεσσαλονίκης - Χαλκιδικής, στην οποία παίζω με τα μαύρα.
Με μια γρήγορη εκτίμηση της θέσης γίνεται φανερό ότι τα μαύρα είναι πολύ ανώτερα, λόγω της κάκιστης λευκής πιονοδομής και των δύο κεντρικών ελεύθερων μαύρων πιονιών, τα οποία συν τοις άλλοις είναι και δεμένα. Η καλύτερη συνέχεια για τα μαύρα είναι μάλλον 1...Rf1 με την απλή ιδέα 2...Ra1 μαζεύοντας τα σκόρπια λευκά πιόνια, χωρίς το παραμικρό αντάλλαγμα για τα λευκά. Για παράδειγμα, στο 2. Rg6+ Ke5! (και όχι 2...Rf6) με συντριπτική επίθεση στον λευκό βασιλιά. Π.χ., 3. Rxa6 e3+, κτλ.
Το πρώτο μου σφάλμα στην παρτίδα είναι ότι παραμέρισα αυτήν τη φυσιολογική συνέχεια και ενέδωσα σε μια κάκιστη σκακιστική ή αλλιώς «σκάκιστη» - για να χρησιμοποιήσω ένα προσωπικό λογοπαίγνιο - συνήθεια που έχω, να μετράω ατελείωτες βαριάντες εκεί που δεν χρειάζεται. Το αποτέλεσμα είναι ουκ ολίγες φορές να μου ξεφεύγει κάποια ενδιάμεση κίνηση του αντιπάλου σε μεγάλο βάθος της βαριάντας, η οποία μάλιστα στη ροή του παιχνιδιού μπορεί και να είναι οφθαλμοφανέστατη, με αποτέλεσμα ακόμη και να χάνω την παρτίδα. Στη θέση αυτή λοιπόν εκτίμησα ότι μπορώ με τη στρατηγική θυσία ενός πιονιού να μπω με φορσέ τρόπο σε κερδισμένο φινάλε.
Το πρώτο μου σφάλμα στην παρτίδα είναι ότι παραμέρισα αυτήν τη φυσιολογική συνέχεια και ενέδωσα σε μια κάκιστη σκακιστική ή αλλιώς «σκάκιστη» - για να χρησιμοποιήσω ένα προσωπικό λογοπαίγνιο - συνήθεια που έχω, να μετράω ατελείωτες βαριάντες εκεί που δεν χρειάζεται. Το αποτέλεσμα είναι ουκ ολίγες φορές να μου ξεφεύγει κάποια ενδιάμεση κίνηση του αντιπάλου σε μεγάλο βάθος της βαριάντας, η οποία μάλιστα στη ροή του παιχνιδιού μπορεί και να είναι οφθαλμοφανέστατη, με αποτέλεσμα ακόμη και να χάνω την παρτίδα. Στη θέση αυτή λοιπόν εκτίμησα ότι μπορώ με τη στρατηγική θυσία ενός πιονιού να μπω με φορσέ τρόπο σε κερδισμένο φινάλε.
1...Rf2+? λοιπόν αντί για το ορθό 1...Rf1. Πώς κάνετε έτσι για ένα τετράγωνο...
Τη στιγμή αυτή, όσοι θεατές από την ομάδα μου παρακολουθούσαν την παρτίδα, με κοίταξαν στα μάτια πιστεύοντας ότι έχω κάνει αβλεψία ή ότι μου γλίστρησε ο πύργος και έμεινε σε λάθος τετράγωνο! Εδώ που τα λέμε, αν ήταν έτσι θα είχα και μια καλή δικαιολογία... Η κίνηση αυτή όμως παίχτηκε σκόπιμα και κρύβει μέσα της πολύ μεγάλο βάθος. Τόσο μεγάλο που κατάπιε κι εμένα τον ίδιο... Ακολούθησε
2. Rxf2 e3+, 3. Ke2 exf2
Πήρα πίσω τον πύργο θυσιάζοντας προσωρινά ένα πιόνι για να μπω σε ένα κλασικό φινάλε δεμένου ελεύθερου πιονιού εναντίον μακρινού ελεύθερου. Εν γένει, το πλεονέκτημα του δεμένου ελεύθερου είναι τόσο μεγάλο που ακόμη και με πιόνι κάτω, σε συγκεκριμένες θέσεις και υπό ορισμένες προϋποθέσεις (π.χ., διπλωμένα πιόνια του αντιπάλου) δίνει τη δυνατότητα νίκης (βλέπε... την παρτίδα που βλέπεις). Έτσι λοιπόν, στη θέση αυτή, εκτίμησα ότι τα διπλωμένα πιόνια του λευκού στην a στήλη λογαριάζονται ως ένα και συνεπώς το πλεονέκτημα του δεμένου ελεύθερου θα πρέπει να είναι αρκετό για τη νίκη. Το σχέδιό μου είναι να χρησιμοποιήσω για αντιπερισπασμό το ελεύθερο πιόνι στο d4 με σκοπό να πάρω το λευκό πιόνι στο h2 και να κερδίσω την οποζισιόν1 σπρώχνοντας το λευκό βασιλιά μακριά από την άμυνα των υπόλοιπων λευκών πιονιών.
Όλα αυτά συμφωνούν με το γενικό κανόνα. Δεν μου πέρασε από το μυαλό όμως ο μεγαλύτερος εχθρός ενός κανόνα, η εξαίρεση... Και δυστυχώς η θέση αυτή αποτελεί εξαίρεση. Το πρόβλημα για τα μαύρα είναι το πιόνι στο a2 το οποίο όπως θα δούμε σώζει την τελευταία στιγμή στην κυριολεξία τα λευκά! Πιο συγκεκριμένα, όταν τα μαύρα αιχμαλωτίσουν το λευκό πιόνι στο c4 και σπρώξουν το μαύρο πιόνι από το c5 στο c2, ο λευκός θα έχει πάντα ένα πολύτιμο τέμπο με το πιόνι στο a2 που είναι αρκετό για να του εξασφαλίσει την ισοπαλία με τη βοήθεια του πατ! Δια του λόγου το αληθές, μια πιθανή βαριάντα θα μπορούσε να είναι η επόμενη:
4. Kxf2 (και το 4. a5 οδηγεί σε ισοπαλία με παρόμοια συνέχεια) a5, 5. Ke2 Ke5, 6. Ke1
Κερδίζοντας τη μακρινή οποζισιόν!
6...Kf5, 7. Kf1
Διατηρώντας τη μακρινή οποζισιόν...
7...Kg4, 8. Kg2 Kh4, 9. Kf1 Kh3, 10. Kg1.
Εδώ, αν τα μαύρα είχαν ένα έξτρα τέμπο, θα κέρδιζαν αφού θα ανάγκαζαν τα λευκά να παίξουν είτε 11. a3 είτε 11. Kh1 και στα δύο από τα οποία θα ακολουθούσε 11...d3 (κρατείστε αυτήν την παρατήρηση για αργότερα). Όμως δεν το έχουν και ο μόνος τρόπος για να κάνουν πρόοδο είναι ο επόμενος:
10...d3, 11. Kf2 Kxh2, 12. Ke3 Kg3, 13. Kxd3 Kf3, 14. Kd2 Ke4, 15. Kc3 Ke3, 16. Kc2 Kd4, 17. Kb3 Kd3, 18. Kb2 Kxc4, 19. Kc2
Τώρα υπάρχουν δύο επιλογές:
α) 14...Kd4, 15. Kd2 c4, 16. Kc2 c3, 17. Kd1! (και όχι 17. Kc1? Kd3, 18. Kd1 c2+, 19. Kc1 Kc3, 20. a3 Kd3, 21. Kb2 Kd2 με τετριμμένη νίκη για τα μαύρα. Παρατηρούμε ότι σε αυτήν τη βαριάντα ο λευκός θα προτιμούσε να μην έχει το πιόνι στο a2!)
17...Kd3, 18. Kc1 c2, 19. a3 Kc3 πατ.
β) 14...Kb4, 15. Kd3 Kxa4 (ή 15...c4+, 16. Kd4 c3, 17. Kd3 με ισοπαλία. Προσέξτε το ρόλο του a2 πιονιού το οποίο κρατάει το μαύρο βασιλιά μακριά από το σημαντικό b3 τετράγωνο), 16. Kc4 Ka3, 17. Kxc5 Kxa2, 18. Kb5 νούλα.
Η πραγματική παρτίδα συνεχίστηκε ως εξής:
4. Kxf2 Kf5, 5. Kf3 Kg5, 6. Kg3 Kh5, 7. h4??
Τραγικό λάθος που δίνει τη νίκη στα μαύρα!
7...a5!
Υποχρεώνει τα λευκά να παίξουν την ανεπιθύμητη κίνηση 8. a3, που τους στερεί το πολυπόθητο τέμπο. Διαφορετικά, αν 8. Kh3 ο λευκός βασιλιάς βγαίνει έξω από το τετράγωνο d4-g4-g1-d1 και συνεπώς μετά από 8...d3 δεν προλαβαίνει την προαγωγή του πιονιού.
8. a3 d3, 9. Kf3 Kxh4
Αποκαθιστώντας την υλική ισότητα.
10. Ke3 Kg3, 11. Kxd3 Kf3
Κερδίζοντας την οποζισιόν.
12. Kd2 Ke4, 13. Kc3 Ke3
Διατηρώντας την οποζισιόν.
14. Kc2 Kd4, 15. Kd2 Kxc4
Αποκαθιστώντας για δεύτερη φορά την υλική ισορροπία. Ακολούθησε
16. Kc2 Kd4, 17. Kd2 c4, 18. Kc2 c3
Τώρα αν 19. Kb1 ή 19. Kd1, ο Μαύρος κερδίζει αμέσως με 19...Kd3, 20. Kc1 c2, 21. Kb2 Kd2 κτλ. Οπότε...
19. Kc1
Στη θέση αυτή, παίχτηκε μια τραγωδία που θα τη ζήλευε ακόμη κι ο Αισχύλος! Για κάποιον ανεξήγητο λόγο έχουν αρχίσει να με ζώνουν τα φαντάσματα. Ο νους μου έχει πέσει σε λήθαργο, λαϊκιστί έχω κάψει φλάντζα, κι έχει χαθεί παντελώς η επικοινωνία με τη σκακιέρα. Είμαι βέβαιος ξαφνικά ότι τελικά έχω μετρήσει λάθος και ότι στη θέση αυτή δεν μπορώ να κερδίσω και η απογοήτευση εξουσιάζει το θυμικό μου. Εν τω μεταξύ, ήδη εδώ και μερικές κινήσεις μου ζητείται επίμονα από τον αντίπαλο ισοπαλία, με τρόπο μάλιστα επιτακτικό, για να μην πω περιφρονητικό, κάτι που ήδη έχει αρχίσει να με κάνει να νιώθω άβολα που συνεχίζω να παίζω μια δήθεν «ισόπαλη» θέση (το δίλημμα που λέγαμε...). Τονίζω ότι αυτό σε καμία περίπτωση δεν με απαλλάσσει από την ευθύνη των αποφάσεών μου. Αφού σκέφτηκα για λίγο, δέχτηκα ισοπαλία. Φυσικά, δεν άργησα να καταλάβω τι έκανα. Μα την αλήθεια, ξέχασα να κερδίσω αυτήν την παρτίδα... Το συναίσθημα είναι χειρότερο κι από εκείνο μιας ταπεινωτικής ήττας (αν υπάρχει τέτοια...).
Εδώ τα μαύρα με λίγη γεωμετρία πηγαίνουν πάσο και κερδίζουν με τον εξής «τριγωνικό» τρόπο:
19...Kc5, 20. Kd1 Kd5, 21. Kc1 Kd4
Επαναφέροντας την ίδια με πριν θέση (προσέξτε το τρίγωνο c5-d5-d4 του μαύρου Βασιλιά). Αυτή τη φορά όμως είναι σειρά του λευκού να παίξει.
22. Kc2 Kc4, 23. Kc1 Kb3, 24. Kb1 Kxa3, 25. Kc2 Kb4, 26. Kb1 Kxa4 κτλ.
Σημειωτέον, η θέση αποτελεί βασικό φινάλε που διδάσκεται ακόμη και σε τμήματα αρχαρίων και αν μου είχε ζητηθεί να τη λύσω στο πλαίσιο ενός σκακιστικού παζλ, θα την έλυνα σε ελάχιστο χρόνο. Όμως, η φόρτιση της στιγμής σε συνδυασμό με την επιμονή του αντιπάλου μου να ζητάει ισοπαλία και η βύθιση στο μέτρημα ατελείωτων βαριαντών, θόλωσαν τη σκέψη μου και μου στέρησαν τη νίκη και μισό βαθμό. Για την ιστορία, ευτυχώς η απώλεια αυτή δεν στοίχισε στην ομάδα μου.
Ξεπερνώντας το φιάσκο, όταν επέστρεψα στο σπίτι άρχισα να αναλύω την παρτίδα με παραγωγική πλέον διάθεση και προς μεγάλη μου έκπληξη διαπίστωσα ότι η θέση που προέκυψε μετά τη λάθος μου απόφαση να μπω σε φινάλε (βλ. Διάγραμμα 1), έχει ιδιαίτερο διδακτικό ενδιαφέρον. Όπως ήδη διαπιστώσαμε, τον λευκό σώζει το έξτρα τέμπο που του εξασφαλίζει το πιόνι a2. Τι θα γινόταν λοιπόν αν αλλάζαμε λίγο τη θέση και τοποθετούσαμε ένα επιπλέον πιόνι στο c7 για τα μαύρα (βλ. Διάγραμμα 2);
Τότε μετά από την ίδια συνέχεια
4. Kxf2 a5!, 5. Ke2 Ke5, 6. Ke1 Kf5, 7. Kf1 Kg4, 8. Kg2 Kh4, 9. Kf1 Kh3, 10. Kg1
υπάρχει η κίνηση «ρεζέρβα» 10...c6 η οποία αναγκάζει τα λευκά να παίξουν 11. a3 ή 11. Kh1 και τα δυο από τα οποία χάνουν με 11...d3. Συνεπώς, τα μαύρα με την προσθήκη ενός φαινομενικά αδιάφορου πιονιού φαίνεται ότι θα κέρδιζαν... ή μήπως όχι;
Στην πραγματικότητα, ακόμη και το πιόνι στο c7 δεν είναι αρκετό για να χαρίσει τη νίκη στα μαύρα, αρκεί τα λευκά να ανακαλύψουν μια εκπληκτική ιδέα που κρύβει η θέση. Στη θέση του Διαγράμματος 2, τα λευκά αντί για το προφανές 4. Kxf2 πρέπει να παίξουν το μοναδικό
4. a5! Ke5, 5. Kxf2 Kf4, 6. h3 Kg5, 7. Kg1 Kh5, 8. Kf1 Kh4, 9. Kg2
9...d3, 10. Kf3 Kxh3, 11. Ke3 Kg3, 12. Kxd3 Kf3, 13. Kd2 Ke4, 14. Kc3 Ke3, 15. Kc2 Kd4, 16. Kb3 Kd3
17. a3! c6
18. Ka4!!
Ισοπαλία! Ο λευκός βασιλιάς κρύβεται στη φωλιά που έχτισε μόνος του με τις κινήσεις a5 και a3 και προκαλεί το μαύρο να αγγίξει το ηλεκτροφόρο πιόνι στο c4. Το 18...Kxc4 είναι φυσικά πατ. Όμοια και τα 18...Kc3, 18...Kc2. Επίσης σε οποιαδήποτε οπισθοχώρηση του μαύρου, ο λευκός βασιλιάς ξετρυπώνει από το b3! Ο μαύρος είναι υποχρεωμένος να αποδεχτεί το μοιραίο.
Πολύ ενδιαφέρουσα συνέχεια, με σπάνιας ομορφιάς τελική εικόνα ισοπαλίας. Παίρνοντας λοιπόν τα πράγματα από την αρχή, το άρθρο αυτό θα μπορούσε να ξεκινάει ως εξής: «Με μεγάλη μου χαρά σας παρουσιάζω το επόμενο καλλιτεχνικό φινάλε2 (βλ. Διάγραμμα 2), στο οποίο παίζουν τα μαύρα και κερδίζουν ή παίζουν τα λευκά και κάνουν ισοπαλία!» Το κλειδί στη λύση είναι φυσικά όπως είδαμε ποιος θα προλάβει να παίξει πρώτος a5!
Συνοψίζοντας, η απώλεια της νίκης αυτής της παρτίδας ήταν οδυνηρή. Ωστόσο, η ομορφιά αυτής της αναπάντεχης εικόνας του πατ που προέκυψε από την ανάλυση κατάφερε τουλάχιστον να μου χρυσώσει το χάπι. Αναρωτιέμαι λοιπόν, αν δεν είχα κάνει το λάθος να μπω στο δαιδαλώδες αυτό φινάλε, πώς θα δινόταν η ευκαιρία να γίνουμε μάρτυρες αυτής της εντυπωσιακής σπουδής; Νομίζω ότι αρχίζω να νιώθω υπερήφανος για το λάθος μου...
Ηθικό δίδαγμα: Μην ντρέπεστε για τα λάθη σας. Μοιραστείτε τα με τους άλλους. Αξιοποιήστε τα με παραγωγικό τρόπο και θα βγείτε σίγουρα κερδισμένοι.
1Οποζισιόν (γαλ.) είναι η κατάσταση εκείνη στην οποία οι δύο βασιλιάδες βρίσκονται αντικριστά στην ίδια γραμμή ή στήλη και μεσολαβεί ένα τετράγωνο (περιττός αριθμός τετραγώνων στη μακρινή οποζισιόν) ανάμεσά τους. Ο παίκτης που κατέχει την οποζισιόν, είναι εκείνος του οποίου δεν είναι η σειρά να παίξει. Η οποζισιόν αποτελεί σημαντικό πλεονέκτημα στα φινάλε, καθώς ο παίκτης του οποίου είναι σειρά να παίξει είναι αναγκασμένος να μετακινήσει το βασιλιά του πρώτος, παραχωρώντας την κατάληψη κρίσιμων τετραγώνων από τον αντίπαλο. Το πλεονέκτημα της οποζισιόν μάλιστα είναι τόσο σημαντικό που πολλές φορές είναι αρκετό για να αποφέρει τη νίκη.
2Καλλιτεχνικό φινάλε ή σπουδή είναι μία σκακιστική σύνθεση στην οποία παίζει η μία παράταξη και κερδίζει ή πετυχαίνει ισοπαλία με όποιον τρόπο κι αν απαντήσει ο αντίπαλος.