Πώς να κλείσετε μια θέση ώστε να την ξανανοίξετε αργότερα

Η επόμενη θέση προέρχεται από μια παρτίδα μου στον ιστότοπο lichess.org, στην οποία παίζω με τα μαύρα. Η θέση από άποψη υλικού είναι ισόπαλη, στην πραγματικότητα όμως τα λευκά βρίσκονται κομμάτι κάτω, αφού ο Ίππος τους στο h4 δεν θα ξαναπαίξει ποτέ, καθώς δεν υπάρχουν διαθέσιμα τετράγωνα γι αυτόν! Κατά κανόνα, η στρατηγική της παράταξης που υπερτερεί σε υλικό καθορίζεται από την προσπάθεια να ανοίξει τη θέση, ώστε να εκμεταλλευτεί το επιπλέον υλικό. Στο παρακάτω διάγραμμα, η μόνη ελπίδα των λευκών για ισοπαλία είναι να κλείσει με κάποιον τρόπο η θέση. Με βάση αυτή τη διαπίστωση, η επόμενη μου κίνηση δείχνει παράλογη.

5...c4!?

Προς μεγάλη έκπληξη (εικάζω) του αντίπαλού μου, στο σημείο αυτό αποφάσισα να του κάνω τη χάρη και να κλείσω οικειοθελώς τη θέση, με σκοπό να την ανοίξω προς όφελός μου αργότερα, με την ησυχία μου!

6.Qd1 Nf6, 7.a4 a6!

Τυπική κίνηση η οποία εξασφαλίζει το κλείσιμο στην πτέρυγα της Βασίλισσας. Όποιο από τα a και b λευκά πιόνια κι αν προωθηθεί, τα μαύρα θα κλείσουν αυτόματα τη θέση μετακινώντας το αντίθετο πιόνι. Πιο συγκεκριμένα, στο 8.a5 ακολουθεί 8...b5, ενώ στο 8.b5 ακολουθεί 8...a5.

8.Kh2

Φανερά τα λευκά δεν έχουν κανένα απολύτως σχέδιο.

8...Ne4

Ο Ίππος έφτασε στο ιδανικό του τετράγωνο, από το οποίο «επιτηρεί» τη θέση των λευκών.

9.Qe1 Rh8, 10.Qc1 Rag8

Οι μαύροι Πύργοι καταλαμβάνουν τις βέλτιστες θέσεις και προετοιμάζονται για την εισβολή, η οποία στην παρούσα φάση δείχνει να βρίσκεται μόνο στη σφαίρα της φαντασίας...

11.Rd1 Kf8

Είναι χαρακτηριστικό των κλειστών θέσεων να προσφέρουν την άνεση για αργή ανασύνταξη των δυνάμεων. Προτού επιχειρήσω στην επίθεση θέλω να σιγουρευτώ ότι δεν θα κινδυνέψει ο Βασιλιάς μου όταν ανοίξει η θέση.

12.a5 b5!

Η στρατηγική που ακολουθώ δείχνει εντελώς παράλογη, καθώς η θέση μοιάζει να έχει νεκρώσει. Ωστόσο, έχω ήδη εντοπίσει μια δυνατότητα να «αναστήσω» τη θέση.

13.Re1 Nf2?

Μια κίνηση χωρίς νόημα. Ο Ίππος «ανήκει» στο e4.

14.Re2

Τα λευκά θα μπορούσαν να παίξουν και το πονηρό 14.Ra2, προκαλώντας την απάντηση 14...Nd3, 15.Qd1 Nxe1??, 16.Qxe1, και τα μαύρα, παρά το υλικό τους πλεονέκτημα, δεν υπάρχει τρόπος να κερδίσουν τη θέση, καθώς οι μαύροι Πύργοι είναι εντελώς άχρηστοι.

14...Ne4

Διόρθωσα την προηγούμενη αστοχία.

15.Qc2 Rg5!!

Αυτή είναι η κίνηση κλειδί που οδηγεί τα λευκά στον όλεθρο! Ο Πύργος δεν κόβεται! Αν 16.fxg5? hxg5, 17.Rh1 gxh4 και η «h» στήλη ανοίγει σε κάθε περίπτωση, π.χ. 18.Kg1 Nxg3, κατά τη γνώμη μου η πιο απλή συνέχεια, αν και οι σκακιστικές μηχανές προκρίνουν κινήσεις όπως 18...Qf6 και 18...Rh7. 

16.Rc1 Rh5

Όλα είναι έτοιμα πια για τη διάλυση της λευκής άμυνας.

17.Ree1 Rxh4!?

Ακόμη πιο αποτελεσματικό θα ήταν το 17.Nxg3!. Φυσικά, αν 18.Kxg3 Qxh4#

18.gxh4 Qxh4, 19.Kg1 g3!

Τα λευκά κομμάτια ασφυκτιούν!

20.Kf1 Qh1+, 21.Ke2 Qxg2+

Ο λευκός Βασιλιάς με φορσέ κινήσεις αναγκάζεται σε επικίνδυνο εγκλεισμό στο d1.

22.Kd1 Nf2+, 23.Kd2 h5

Με τα λευκά κομμάτια να στερούνται κινήσεων, τα μαύρα αρπάζουν την ευκαιρία να προωθήσουν το «h» πιόνι.

24.Re2 Ne4+, 25.Kd1 Qg1+, 26.Re1 Nf2+, 27.Ke2 Qg2

Τα μαύρα με μια σειρά δοκιμαστικών κινήσεων, ουσιαστικά αναδιάταξαν τις θέσεις του λευκού Βασιλιά και του λευκού Πύργου.

28.Rg1 Qh3, 29.Rcf1 Qg4+

Η μαύρη Βασίλισσα τοποθετείτε πίσω από τα πιόνια, τα οποία είναι πλέον ασταμάτητα.

30.Ke1 Nd3+, 31.Kd2 h4, 32.Qd1

Τα λευκά προτείνουν την αλλαγή των Βασιλισσών η οποία γίνεται αποδεκτή με ευχαρίστηση.

32...Qxd1+, 33.Kxd1 Nf2+, 34.Ke2 Ne4, 35.Rf3 Nxc3+

Η κατάσταση για τα λευκά είναι εντελώς απελπιστική, ωστόσο συνέχισαν να παίζουν για μερικές ακόμη κινήσεις.

36.Kd2 Ne4+, 37.Ke2 h3, 38.Kf1 g2+, 39.Rxg2 hxg2+, 40.Kxg2

και στο σημείο αυτό τα λευκά εγκατέλειψαν.

Όλοι οι φυσικοί αριθμοί είναι στρόγγυλοι: Ένας εναλλακτικός ορισμός των πρώτων αριθμών

Αν η μεζούρα μου έχει ακρίβεια εκατοστού (cm), έχει νόημα να πω ότι το ύψος μου είναι \(1784\) χιλιοστά (mm);

Στο άρθρο «Η τάξη μεγέθους και το μέγεθος της τάξης» παρουσιάσαμε μια ειδική μορφή στρογγυλοποίησης, η οποία μας επιτρέπει να εκτιμούμε την τάξη μεγέθους ενός συνόλου ή αντικειμένου. Είδαμε επίσης ότι η τάξη μεγέθους είναι άρρηκτα συνδεδεμένη με το αριθμητικό σύστημα που χρησιμοποιούμε. Στο άρθρο αυτό, θα δούμε άλλη μια χρήσιμη εφαρμογή της (συνήθους αυτή τη φορά) στρογγυλοποίησης, με τη βοήθεια της οποίας θα καταλήξουμε σε έναν εναλλακτικό ορισμό των πρώτων φυσικών αριθμών.

Στις φυσικές επιστήμες, για την έκφραση κάποιου μεγέθους, σημαντικότατο ρόλο παίζει η ακρίβεια του οργάνου μέτρησης, η οποία αναφέρεται πολλές φορές και ως διακριτική ικανότητα. Οποιαδήποτε απόδοση μιας μέτρησης με μονάδες μικρότερες της διακριτικής ικανότητας του οργάνου είναι ανούσια, καθώς ενέχει την πιθανότητα σφάλματος. Σε τέτοιες περιπτώσεις συνήθως καταφεύγουμε στη συνήθη διαδικασία της στρογγυλοποίησης η οποία περιγράφεται παρακάτω:

Αλγόριθμος στρογγυλοποίησης

• Βήμα 1ο: Προσδιορίζουμε την τάξη στην οποία θα γίνει η στρογγυλοποίηση. (Στη δική μας περίπτωση, η τάξη αυτή καθορίζεται από τη διακριτική ικανότητα της μεζούρας)
• Βήμα 2ο: Εξετάζουμε το ψηφίο της αμέσως μικρότερης τάξης
• Περίπτωση 1η: Αν είναι μικρότερο του \( 5 \), τότε προχωράμε στο Βήμα 3ο
• Περίπτωση 2η: Αν είναι μεγαλύτερο ή ίσο του \( 5 \), τότε το ψηφίο της τάξης στρογγυλοποίησης αυξάνεται κατά 1
• Βήμα 3ο: Τα ψηφία όλων των τάξεων που είναι μικρότερες της τάξης στρογγυλοποίησης μηδενίζονται

Στην δική μας περίπτωση, η μεζούρα είναι βαθμονομημένη σε cm και άρα δεν μπορεί να «διακρίνει» μήκη μικρότερα του ενός cm. Γι αυτόν τον λόγο οφείλουμε να κάνουμε στρογγυλοποίηση στην τάξη των cm. Καθώς το ψηφίο \(4\) που ανήκει στην τάξη των mm είναι μικρότερο του \(5\), η μέτρηση στρογγυλοποιείται σε \(1780\). Έτσι, είναι ορθότερο να πω ότι το ύψος μου είναι \(1780\) mm ή απλούστερα \(178\) cm.

Βασισμένοι τώρα στην έννοια της στρογγυλοποίησης, θα δώσουμε έναν εναλλακτικό ορισμό των πρώτων ακεραίων αριθμών. Για το σκοπό αυτό, δίνουμε τον επόμενο τετριμμένο ορισμό:

Ορισμός 1: Ένας ακέραιος αριθμός καλείται στρόγγυλος όταν το τελευταίο του ψηφίο είναι το μηδέν.

Στο φως αυτού του ορισμού, ας προσπαθήσουμε να απαντήσουμε στην επόμενη ερώτηση:

Ποιοι από τους επόμενους φυσικούς αριθμούς είναι στρόγγυλοι;

\( 0, 5, 9, 10, 19, 20, 97, 100 \)

Δεν νομίζω να υπάρχει αμφιβολία ότι η αυθόρμητη απάντηση είναι ότι στρόγγυλοι αριθμοί είναι οι \( 0 , 10, 20 \) και \( 100 \). Τα πράγματα όμως δεν είναι τόσο απλά. Για να απαντηθεί το ερώτημα, είναι κρίσιμης σημασίας το αριθμητικό σύστημα που χρησιμοποιούμε. Στο δεκαδικό σύστημα, ασφαλώς οι στρόγγυλοι αριθμοί του παραπάνω συνόλου είναι οι \( 0, 10, 20 \) και \( 100 \). Ο αριθμός \( 9 \) σαφώς δεν είναι στρόγγυλος στο 10-δικό, ωστόσο είναι στρόγγυλος στο 3-δικό αφού εκεί γράφεται ως \( 100 \). Επίσης, είναι στρόγγυλος προφανώς και στο 9-δικό σύστημα, όπου γράφεται ως \( 10 \). Όμοια, το \( 19 \), που είναι και πρώτος αριθμός, είναι ένας ολοστρόγγυλος αριθμός στο 19-δικό σύστημα, αφού γράφεται ως \( 10 \). 

Από τα παραπάνω, μπορούμε να καταλήξουμε σε μερικές πολύτιμες παρατηρήσεις:

Παρατήρηση 1: Κάθε φυσικός αριθμός, στο αριθμητικό σύστημα με βάση τον εαυτό του, γράφεται ως \( 10 \). Συνεπώς, για κάθε φυσικό αριθμό, υπάρχει ένα τουλάχιστον αριθμητικό σύστημα, στο οποίο αυτός είναι στρόγγυλος! Κατά κάποιον τρόπο, θα μπορούσαμε να πούμε ότι όλοι οι φυσικοί αριθμοί είναι στρόγγυλοι, αρκεί να τους δούμε από την κατάλληλη «αριθμητική οπτική γωνία».

Παρατήρηση 2: Μια ακόμη παρατήρηση που πηγαίνει κόντρα στη διαίσθηση είναι ότι το \( 10 \) μπορεί να είναι πρώτος αριθμός! Πράγματι, όπως είδαμε παραπάνω, το \( 10 \) στο 19-δικό σύστημα είναι πρώτος αριθμός.

Παρατήρηση 3: Στην πραγματικότητα, για κάθε φυσικό αριθμό υπάρχουν τόσα αριθμητικά συστήματα στα οποία αυτός είναι στρόγγυλος, όσοι και οι φυσικοί του διαιρέτες, εξαιρουμένου του 1. Πιο συγκεκριμένα, αν \( d \) είναι ένας φυσικός διαιρέτης του φυσικού αριθμού \( a \) διάφορος του 1, τότε ο \( a \) είναι στρόγγυλος στο d-δικό σύστημα¹ και αντιστρόφως. Για παράδειγμα, το \( 12 \) είναι στρόγγυλος αριθμός σε \( 5 \) αριθμητικά συστήματα: στο 2-δικό, στο 3-δικό, στο 4-δικό, στο 6-δικό και στο 12-δικό, καθώς οι φυσικοί διαιρέτες του \( 12 \) είναι οι \( 1, 2, 3, 4, 6 \) και \( 12 \). Δια του λόγου το αληθές παρατίθενται οι εκφράσεις του \( 12 \) σε όλα τα αριθμητικά συστήματα με βάση από το \( 2 \) έως το \( 12 \):

Στα συστήματα με βάση μεγαλύτερη του \( 12 \) είναι προφανές ότι το \( 12 \) παύει να είναι στρόγγυλος αριθμός.

Συνδυάζοντας τις τρεις προηγούμενες παρατηρήσεις μπορούμε να καταλήξουμε στο επόμενο θεώρημα, το οποίο μπορεί να θεωρηθεί και ως ένας εναλλακτικός ορισμός των πρώτων αριθμών. 

Θεώρημα (Εναλλακτικός ορισμός των πρώτων αριθμών): Πρώτος είναι ένας φυσικός αριθμός \(p\), για τον οποίο ισχύει ότι η ελάχιστη αριθμητική βάση στην οποία είναι στρόγγυλος είναι το \(p\).

Απόδειξη:

Με βάση την Παρατήρηση 1 και 2, ο \(p\) στο αριθμητικό σύστημα με βάση \(p\) είναι στρόγγυλος. Από την Παρατήρηση 3 όμως εγκαθιδρύεται μια πλήρης αντιστοιχία ανάμεσα στους διαιρέτες του \(p\) και στις αριθμητικές βάσεις στις οποίες ο \(p\) είναι στρόγγυλος. Με άλλα λόγια, το \(d\) είναι διαιρέτης του \(p\) αν και μόνο αν ο \(p\) είναι στρόγγυλος στο \(d\)-δικό σύστημα. Με βάση τα παραπάνω, προχωράμε στην απόδειξη του θεωρήματος:

(\( \Rightarrow \)): Έστω \(p\) ένας πρώτος αριθμός. Από τον ορισμό των πρώτων, οι μόνοι διαιρέτες του \(p\) είναι το \(1\) και το \(p\). Εφόσον ο \(p\) δεν έχει διαιρέτες που να είναι μικρότεροι του \(p\) και ταυτόχρονα μεγαλύτεροι του \(1\), ο \(p\) δεν είναι στρόγγυλος σε καμία αριθμητική βάση \(d\) με \( 2 \le d \le p-1 \). Συνεπώς, η ελάχιστη αριθμητική βάση στην οποία ο \(p\) είναι στρόγγυλος είναι το \(p\).

(\( \Leftarrow \)): Αντιστρόφως. Έστω ότι η ελάχιστη αριθμητική βάση στην οποία ο \(p\) είναι στρόγγυλος είναι το \(p\). Ας υποθέσουμε ότι ο \(p\) δεν είναι πρώτος, άρα έχει έναν τουλάχιστον διαιρέτη \(d\) με \( 2 \le d \le p-1 \). Αυτό σημαίνει ότι ο \(p\) είναι στρόγγυλος στο αριθμητικό σύστημα με βάση \(d\). Συνεπώς, το \(p\) δεν είναι η ελάχιστη βάση στην οποία ο \(p\) είναι στρόγγυλος. Καταλήγουμε δηλαδή σε άτοπο, το οποίο σημαίνει ότι ο \(p\) είναι πρώτος αριθμός.

Κλείνοντας, παρέχουμε μερικές επιπλέον χρήσιμες παρατηρήσεις καθώς και μερικά παραδείγματα στα οποία γίνεται χρήση του θεωρήματος αυτού:

Παρατήρηση 4: Προφανώς, κάθε άρτιος αριθμός μεγαλύτερος του \( 2 \) είναι στρόγγυλος στο δυαδικό σύστημα, συνεπώς δεν είναι πρώτος. 

Παρατήρηση 5: Η έκφραση κάθε αριθμού \( a \) σε οποιοδήποτε αριθμητικό σύστημα με βάση \( b \), τέτοια ώστε \( \frac{a}{2} < b < a \) είναι \( (1 (a-b))_b \). Για παράδειγμα, η έκφραση του \( a=13 \) στο \(8\)-δικό είναι \( 15 \), δεδομένου ότι \( a-b=5 \). Στην προσπάθεια να διαπιστώσουμε αν ένας αριθμός \( a \) είναι πρώτος, η παρατήρηση αυτή μας επιτρέπει να εξετάσουμε αν ο αριθμός αυτός είναι στρόγγυλος στα αριθμητικά συστήματα με βάση από \( 2 \) έως τον μεγαλύτερο φυσικό που είναι μικρότερος του \( \frac{a}{2} \). Φυσικά, θα πρέπει να αναφέρουμε ότι ακόμη καλύτερα, σύμφωνα με γνωστό θεώρημα της θεωρίας αριθμών, η διαδικασία εύρεσης μιας βάσης στην οποία ο \( a \) είναι στρόγγυλος μπορεί να περιοριστεί στο διάστημα φυσικών από \( 2 \) έως και \( \sqrt{a} \). 

Παράδειγμα 1: Έστω ο αριθμός \( 13 \) του δεκαδικού συστήματος. Οι εκφράσεις του \( 13 \) στα διάφορα συστήματα είναι οι εξής:

Είναι φανερό ότι για καμία βάση μικρότερη του \( 13 \), ο αριθμός \( 13 \) δεν είναι στρόγγυλος. Συνεπώς, με βάση τον Ορισμό 2, το \( 13 \) είναι πρώτος αριθμός.

Παράδειγμα 2: Έστω τέλος ο αριθμός \( 15 \) του δεκαδικού συστήματος. Οι εκφράσεις του \( 15 \) στα διάφορα συστήματα είναι οι εξής:

Παρατηρούμε ότι το \( 15 \) είναι στρόγγυλος στα αριθμητικά συστήματα με βάση το \( 3 \) και το \( 5 \), συνεπώς είναι σύνθετος αριθμός.

¹ Το 1 εξαιρείται καθώς δεν νοείται αριθμητικό σύστημα με βάση το 1.

Η τάξη μεγέθους και το μέγεθος της τάξης

Υπάρχει ένα σύντομο μαθηματικό ανέκδοτο που λέει το εξής¹:

Ένας φαντάρος φυλάει σκοπιά στον λόχο του. Κάποια στιγμή διακρίνει στον ορίζοντα μια ένοπλη εχθρική ομάδα να πλησιάζει και τρέχει αμέσως να το αναφέρει στον Λοχαγό του:

«Κύριε Λοχαγέ, δεχόμαστε επίθεση από εχθρούς!»

«Πόσοι είναι;»

«Περίπου 1003!»

Είθισται στην καθημερινή μας πρακτική, όταν θέλουμε να εκτιμήσουμε την τάξη μεγέθους ενός συνόλου, να χρησιμοποιούμε τις δυνάμεις του \( 10 \). Έτσι, για παράδειγμα, μπορούμε χοντρικά να πούμε ότι το πλάτος της ανθρώπινης παλάμης είναι «περίπου» \( 10 \) εκατοστά. Ένα μεγάλο προτέρημα της τάξης μεγέθους είναι ότι μας επιτρέπει να κάνουμε γρήγορες συγκρίσεις ανάμεσα σε δύο ή περισσότερα σύνολα ή αντικείμενα. Αύξηση κατά μία τάξη μεγέθους σημαίνει πολλαπλασιασμό επί \( 10 \), ενώ μείωση κατά μία τάξη μεγέθους σημαίνει διαίρεση δια \( 10 \). Γενικά, αύξηση (μείωση) κατά \( n \) τάξεις μεγέθους σημαίνει πολλαπλασιασμό επί (διαίρεση δια) \( 10^n. \) Για παράδειγμα, η μέση ταχύτητα μετακίνησης από μία πόλη στην άλλη με αυτοκίνητο είναι \( 100 \, km/h \), ενώ αντίστοιχα η μέση ταχύτητα με κάρο είναι \( 10 \, km/h \). Αυτό σημαίνει ότι η εμφάνιση του αυτοκινήτου στον σύγχρονο κόσμο αύξησε τη μέση ταχύτητα μετακίνησης κατά μία τάξη μεγέθους, δηλαδή δεκαπλασίασε περίπου την ταχύτητα σε σχέση με εκείνη του παλαιού κόσμου.

Τυπικά, η τάξη μεγέθους ενός αριθμού \( a \) υπολογίζεται ως εξής: Εκφράζουμε τον αριθμό \( a \) στη μορφή: 

\( a = m \cdot 10^r \), όπου \( \frac{\sqrt{10}}{10} \le m < \sqrt{10} \). 

Η τάξη μεγέθους του \( a \) είναι τότε ίση με \( 10^r \).

Παρατηρούμε ότι η τάξη μεγέθους ενός αριθμού συνιστά μια ειδική μορφή στρογγυλοποίησης. Σε αντίθεση με τη συνήθη στρογγυλοποίηση, για τη μετάβαση από μία τάξη μεγέθους (\( 10^r \)) στην επόμενη (\( 10^{r+1} \)) χρησιμοποιείται ως κατώφλι η τιμή \( \sqrt{10} \cdot 10^r \approx 3.162 \cdot 10^r, \) που είναι ο γεωμετρικός μέσος² των τιμών \( 10^r \) και \( 10^{r+1} \). Έτσι, η τάξη μεγέθους του \( 316 \) είναι \( 10^2=100 \), ενώ του \( 317 \) είναι \( 10^3=1000 \), καθώς \( 316 = 3.16 \cdot 10^2 \), ενώ \( 317 = 0.317 \cdot 10^3 \). Προσέξτε ότι δεν θα μπορούσαμε να γράψουμε \( 316 = 0.316 \cdot 10^3 \), διότι \( 0.316 < \frac{\sqrt{10}}{10} \). Επίσης, δεν θα μπορούσαμε να γράψουμε \( 317 = 3.17 \cdot 10^2 \), διότι \( \sqrt{10} < 3.17 \).

Ας επιστρέψουμε όμως στο ανέκδοτο. Αν και απεχθάνομαι την εξήγηση του λόγου για τον οποίο ένα ανέκδοτο είναι αστείο, χάριν του άρθρου θα πρέπει να κάνω μια εξαίρεση. Αυτό λοιπόν που κάνει αστείο το παραπάνω ανέκδοτο (ήδη αισθάνομαι τσακισμένος από αυτό που επιχειρώ να κάνω) είναι ότι ο φαντάρος προσπαθεί να δώσει την τάξη μεγέθους του πλήθους των εχθρών «στρογγυλοποιώντας» τον εκτιμώμενο αριθμό στη «μη-στρόγγυλη» τιμή \( 1003 \). Όμως, υπάρχει κάτι σημαντικό εδώ. Το ανέκδοτο είναι αστείο μόνο εφόσον σκεφτόμαστε στο δεκαδικό σύστημα και εξηγώ αμέσως τι εννοώ.

Ας μεταφέρουμε το σκηνικό με τον φαντάρο και τον Λοχαγό σε έναν υποτιθέμενο πλανήτη, στον οποίο κατοικεί ένας πολιτισμός που υιοθετεί το 17-δικό σύστημα αρίθμησης. Στο 17-δικό σύστημα ο αριθμός \( 1003 \) εκφράζεται ως \( 380 \), αφού εύκολα προκύπτει ότι 

\( (1003)_{17} = 3 \times 17^2 + 8 \times 17^1 + 0 \times 17^0 \) 

Σε αυτή την περίπτωση, ο διάλογος μετατρέπεται στον εξής:

«Κύριε Λοχαγέ, δεχόμαστε επίθεση από εχθρούς!»

«Πόσοι είναι;»

«Περίπου 380!»

Αναμφίβολα, στον πλανήτη αυτό, το ανέκδοτο χάνει λίγη από την αίγλη του.

Παρόμοια είναι η κατάσταση αν ο πολιτισμός υιοθετεί το 59-δικό σύστημα. Τότε, καθώς 

\( (1003)_{59} = 17 \times 59^1 + 0 \times 59^0 \) 

ο διάλογος μετατρέπεται στον εξής: 

Άλλη μια φορά τη σκηνή. Φώτα! Κάμερα! Πάμε:

«Κύριε Λοχαγέ, δεχόμαστε επίθεση από εχθρούς!»

«Πόσοι είναι;»

«Περίπου 170!»³

Τέλος αν ο πολιτισμός αυτός υιοθετεί το 1003-δικό σύστημα, τότε ο διάλογος γίνεται ο εξής: 

Πάμε μια τελευταία φορά το γύρισμα:

«Κύριε Λοχαγέ, δεχόμαστε επίθεση από εχθρούς!»

«Πόσοι είναι;»

«Περίπου 10!»

Φυσικά,

\( (1003)_{1003} = 1 \times 1003^1 + 0 \times 1003^0 \)

και το ανέκδοτο παύει πλέον να είναι ανέκδοτο. 

Από τα παραπάνω διαπιστώνουμε μια άμεση εξάρτηση της αίσθησης του χιούμορ από το αριθμητικό σύστημα που χρησιμοποιούμε! Η πιο σημαντική διαπίστωση όμως είναι ότι η ίδια η έννοια της τάξης μεγέθους εξαρτάται τελικά άρρηκτα από το αριθμητικό σύστημα. Όπως έχουμε ήδη αναφέρει, οι αριθμοί \( 10 \) και \( 100 \) διαφέρουν μία τάξη μεγέθους στο 10-δικό σύστημα. Οι ίδιοι αριθμοί όμως στο δυαδικό σύστημα μεταφράζονται σε \( (1010)_2 \) και \( (1100100)_2 \), που προσεγγιστικά είναι οι \( (1000)_2 \) και \( (10000000)_2 \), οι οποίοι διαφέρουν τέσσερις τάξεις μεγέθους! Στην καθημερινότητά μας συνεπώς κάθε φορά που μιλάμε για την τάξη μεγέθους ενός αντικειμένου, ουσιαστικά κάνουμε τη σιωπηρή υπόθεση ότι αναφερόμαστε στο προσφιλές σε όλους μας 10-δικό σύστημα. 

Είμαστε πλέον σε θέση να δώσουμε τον γενικό ορισμό της τάξης μεγέθους για οποιαδήποτε βάση \( b \). 

Αν εκφράσουμε έναν αριθμό \( a \) στη μορφή:

\( a = m \cdot b^r \), όπου \( \frac{\sqrt{b}}{b} \le m < \sqrt{b} \)

τότε η τάξη μεγέθους του \( a \) ως προς τη βάση \( b \) είναι ίση με \( b^r \).

Για παράδειγμα, στην περίπτωση του δυαδικού συστήματος, ήτοι για \( b=2 \), έχουμε \( \sqrt{2} \approx (1.01101)_2 \), συνεπώς ο αριθμός \( (10110)_2 \) που αντιστοιχεί με το \( 22 \) στο 10-δικό, έχει τάξη μεγέθους \( 4 \), αφού \( (10110)_2 = (1.0110)_2 \cdot 2^4 \), ενώ ο αριθμός \( (10111)_2 \) που αντιστοιχεί με το \( 23 \) στο 10-δικό, έχει τάξη μεγέθους \( 5 \), αφού \( (10111)_2 = (0.10111)_2 \cdot 2^5 \). 

Στον επόμενο πίνακα παραθέτω ενδεικτικά παραδείγματα της «δεκαδικής» τάξης μεγέθους διαφόρων αντικειμένων και αποστάσεων στο Σύμπαν, διατρέχοντας όλο το φάσμα των μεγεθών, από τον μικρόκοσμο στον μακρόκοσμο.

Η τάξη μεγέθους διαφόρων αντικειμένων και αποστάσεων στο Σύμπαν.

Κλείνοντας, θα ήθελα να διηγηθώ μια μικρή ιστοριούλα από τα σχολικά μου χρόνια. Σε μία ονειροπόληση του μυαλού μου, κατά τη διάρκεια ενός μαθήματος το οποίο προφανώς δεν κατάφερε να κερδίσει την προσοχή μου, αναρωτήθηκα πόσο να ζυγίζει άραγε ο αέρας που βρίσκεται μέσα σε μία άδεια τάξη. Φυσικά, δεν με ενδιέφερε να μάθω το ακριβές βάρος του αέρα, αλλά να εκτιμήσω την τάξη μεγέθους του. Είναι της τάξης των γραμμαρίων, του ενός κιλού, των δέκα κιλών, των εκατό κιλών ή μήπως του ενός τόνου; Επειδή ασφαλώς δεν θυμάμαι τις πράξεις που είχα κάνει τότε, θα δοκιμάσω να επαναλάβω εκ νέου την εκτίμησή μου:

Έστω ότι οι διαστάσεις μιας συνηθισμένης τάξης είναι \( 8 \, m \times 8 \, m \times 3 \, m \). Ο όγκος αυτής της τάξης είναι τότε \( 192 \, m^3 \). Χάριν ευκολίας και δεδομένου ότι κάνουμε χονδρικές υποθέσεις ας στρογγυλοποιήσουμε αυτόν τον όγκο στα \( 200 \, m^3 \) ή ισοδύναμα \( 200000 \, lt \). Η γραμμομοριακή μάζα του ατμοσφαιρικού αέρα σε ιδανικές συνθήκες (STP⁴) εκτιμάται στα \( 28,96 \, g/mole \), δηλαδή περίπου \( 30 \, g/mole \), ενώ ο γραμμομοριακός του όγκος είναι \( 22,4 \, lt/mole \), δηλαδή περίπου \( 20 \, lt/mole \). Με απλά λόγια, ένα mole ατμοσφαιρικού αέρα ζυγίζει \( 30 \, g \) και καταλαμβάνει \( 20 \, lt \). Από αυτά τα δεδομένα προκύπτει ότι η τάξη περιέχει \( 200000 \, lt : 20 \, lt/mole = 10000 \, mole \) αέρα, ο οποίος ζυγίζει \( 10000 \, mole \cdot 30 \, g/mole = 300000 \, g = 300 \, Kg = 3 \cdot 10^2 \, Kg \). Διόλου αμελητέο! Βέβαια, αξίζει να σημειώσουμε ότι αν είχε έρθει αντιμέτωπος με την ερώτηση «πόσο ζυγίζει ο αέρας σε μία άδεια τάξη» ο Δημόκριτος, η απάντηση που θα έδινε θα ήταν μάλλον «μηδέν», αφού σε μία άδεια τάξη δεν υπάρχει αέρας!

¹ Το ανέκδοτο αυτό το άκουσα για πρώτη φορά από τον καλό μου φίλο Δημήτρη Γκαρίπη.

² Ο Γεωμετρικός Μέσος δύο αριθμών \( a \) και \( b \) είναι ο \( \sqrt{a \cdot b} \).

³ Για την ακρίβεια, η ορθή έκφραση είναι \( \theta 0 \), αφού το \( 17 \) στο 59-δικό σύστημα συμβατικά συμβολίζεται με \( \theta \). Ωστόσο, στο κείμενο, χάριν ευφωνίας χρησιμοποιείται το κατά τα άλλα λανθασμένο \( 170 \).

⁴ Standard Temperature and Pressure (STP) είναι οι πρότυπες συνθήκες για τη θερμοκρασία T και την πίεση P και ορίζονται ως εξής: Τ: \( 0^{\circ} \)C, P: \( 0,98692 \, atm \).

Οι προπαίδειες

Από μικρή ηλικία μαθαίνουμε την προπαίδεια, τη «μία και μοναδική» προπαίδεια. Για την προπαίδεια έχουν γραφτεί χαριτωμένα παιδικά ποιηματάκια και τραγουδάκια, έχουν δημιουργηθεί όμορφες και εύπεπτες εικόνες, έχουν επινοηθεί έξυπνα τεχνάσματα που χρησιμοποιούν διάφορα μέσα, όπως για παράδειγμα τα δάχτυλα των χεριών, τεμνόμενες γραμμές, κτλ. Όλα αυτά με σκοπό να μάθουν τα παιδιά εύκολα και γρήγορα αυτό το πολύτιμο εργαλείο που θα τους επιτρέψει αργότερα να προχωρήσουν στα μαθηματικά. Ένα πράγμα όμως που άθελά μας παραβλέπουμε είναι ότι η προπαίδεια δεν είναι τελικά «μία και μοναδική». Απεναντίας, υπάρχουν τόσες προπαίδειες, όσοι είναι και οι φυσικοί αριθμοί, δηλαδή άπειρες! Το ότι μαθαίνουμε μόνο μία, οφείλεται αποκλειστικά στο γεγονός ότι εντελώς αυθαίρετα, το ανθρώπινο είδος, ανάμεσα από τα άπειρα αριθμητικά συστήματα, καθένα από τα οποία έχει ως βάση έναν φυσικό αριθμό, έχει επιλέξει να πορευτεί με το δεκαδικό σύστημα, το σύστημα δηλαδή που έχει ως βάση το δέκα.

Για τη διαδικασία εξαγωγής της προπαίδειας με οποιαδήποτε αριθμητική βάση είναι απαραίτητο το επόμενο Θεώρημα και ο επόμενος Ορισμός της Θεωρίας Αριθμών: 

Θεώρημα: Αν b είναι ένας φυσικός αριθμός μεγαλύτερος του 1, τότε κάθε φυσικός αριθμός n>0 έχει μια μονοσήμαντη παράσταση της μορφής 

\[n = n_0 + n_1 b + n_2 b^2 + \dots + n_m b^m\]

όπου \( n_m \ne 0 \) και \( 0 \le n_k < b \) για \( 0 \le k \le m \)

Ορισμός: Η έκφραση του αριθμού n στο b-δικό αριθμητικό σύστημα είναι:

\[n = (n_m n_{m-1} \dots n_1 n_0)_b\]

Για παράδειγμα ο αριθμος 24 στο 7-δικό σύστημα μεταφράζεται ως εξής: 

\[(24)_7 = 2 \times 7^1 + 4 \times 7^0=2 \times 7 + 4\]

όπως φαίνεται εύκολα αν στις σχέσεις του Θεωρήματος και του Ορισμού θέσουμε \(b=7, m=1, n_0=4, n_1=2\). Αξίζει να σημειωθεί ότι στο δεκαδικό σύστημα, χάριν απλότητας παραλείπεται η βάση, ώστε αντί για \( (n_m n_{m-1} \dots n_1 n_0)_{10} \) γράφουμε απλώς \( n_m n_{m-1} \dots n_1 n_0 \). Έτσι για παράδειγμα, αντί για \( (24)_{10} \) γράφουμε απλώς \( 24 \).

Έστω τώρα ότι θέλουμε να υπολογίσουμε το γινόμενο \( 3 \times 6 \) στο 7-δικό σύστημα. Ένας τρόπος να βρούμε το αποτέλεσμα είναι με αναγωγή στο 10-δικό σύστημα:  

\[ 3 \times 6 = 18 = 14 + 4 = 2 \times 7 + 4 = 2 \times 7^1 + 4 \times 7^0 = (24)_7 \]

Ένας πιο στοιχειώδης τρόπος, που είναι ανεξάρτητος από το 10-δικό σύστημα είναι ο εξής:

\[ 3 \times 6 = 6 + 6 + 6 = 6 + (1+5) + 6 = (6+1)+5+6=10+5+6= \]

\[ 10+5+(2+4) = 10+(5+2)+4=10+10+4=2 \times 10+4=20+4=24 \]

Άλλωστε, ακόμη κι αν ίσως δεν το έχουμε συνειδητοποιήσει, αυτός είναι ο τρόπος με τον οποίον γίνεται ο πολλαπλασιασμός και στο 10-δικό σύστημα.

Σε κάθε περίπτωση, βρίσκουμε ότι στο 7-δικό σύστημα \( 3 \times 6 = 24 \). Όσο αυθαίρετο κι αν φαίνεται αυτό το αποτέλεσμα, ας μην ξεχνάμε ότι είναι εξίσου αυθαίρετο με το γεγονός ότι \( 3 \times 6 = 18 \) στο 10-δικό σύστημα. Η «φυσικότητα» του τελευταίου έγκειται καθαρά και μόνο στην τεράστια εξοικείωση που έχουμε με το 10-δικό σύστημα.

Ακολουθώντας την παραπάνω λογική μπορούμε να συμπληρώσουμε την προπαίδεια για όποια βάση επιθυμούμε. Παρακάτω παρουσιάζονται οι προπαίδειες που αντιστοιχούν στα αριθμητικά συστήματα με βάση από το 1 ως το 10.

2-δικό σύστημα.

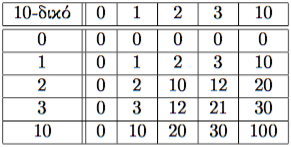
3-δικό σύστημα.

4-δικό σύστημα.

5-δικό σύστημα.

6-δικό σύστημα.

7-δικό σύστημα.

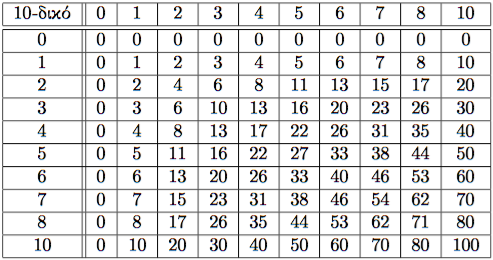
8-δικό σύστημα.

9-δικό σύστημα.

10-δικό σύστημα.

Φυσικά, όπως έχουμε ήδη αναφέρει, η λίστα δεν τελειώνει εδώ και θα μπορούσαμε να συνεχίσουμε με το 11-δικό, το 12-δικό κτλ. Η μόνη διαφορά με τα συστήματα που έχουν βάση μεγαλύτερη του 10 είναι ότι, σε σημειογραφικό επίπεδο, λόγω της εξάντλησης των δέκα γνωστών μας ψηφίων, πρέπει να επινοήσουμε καινούρια σύμβολα για το δέκα, το έντεκα, το δώδεκα, κ.ο.κ. Έτσι, για παράδειγμα, το 10 δεν μπορεί να έχει την έννοια του δέκα στο εντεκαδικό σύστημα, καθώς \( 10 = 1 \times 11 + 0 \), που με όρους δεκαδικού συστήματος είναι το 11. Για αυτό το λόγο, στο εντεκαδικό σύστημα, για το δέκα χρησιμοποιούμε κάποιο νέο σύμβολο, διαφορετικό από τα 0, 1, 2, ..., 9. Είθισται, ως δεξαμενή άντλησης νέων συμβόλων να χρησιμοποιείται το σύνολο των γραμμάτων του αλφαβήτου. Έτσι, για το 10 στο εντεκαδικό σύστημα, είναι βολικό να χρησιμοποιηθεί το «α», για το 11 στο δωδεκαδικό σύστημα το «β», κ.ο.κ. Ασφαλώς είναι φανερό ότι κάποια στιγμή εξαντλούνται τα γράμματα του αλφαβήτου. Στην περίπτωση αυτή είναι αναπόφευκτο να επινοηθούν νέα σύμβολα. Ωστόσο, συστήματα με τόσο μεγάλη βάση δεν έχουν καμία πρακτική αξία για εμάς. Ενδεικτικά, παρακάτω παρουσιάζεται και η προπαίδεια του 11-δικού συστήματος, όπου το δέκα συμβολίζεται με α.

11-δικό σύστημα.

Με βάση τους παραπάνω πίνακες, αξίζει να κάνουμε μερικές χρήσιμες παρατηρήσεις. 

1. Αρχικά, μπορεί εύκολα κανείς να καταλήξει στο εσφαλμένο συμπέρασμα ότι υπάρχει τυπογραφικό λάθος, καθώς σε όλους τους πίνακες γράφει επάνω αριστερά 10-δικό. Στην πραγματικότητα όμως δεν υπάρχει κανένα τυπογραφικό λάθος. Το μυστικό είναι ότι σε κάθε σύστημα η βάση εκφράζεται με το 10. Το κάθε σύστημα στην ουσία διαφέρει μόνο στο πλήθος των ψηφίων που χρησιμοποιεί.
2. Σε όλους τους πίνακες, η δεύτερη γραμμή και η δεύτερη στήλη περιέχει μόνο μηδενικά. Αυτό είναι ασφαλώς συνεπές με το ότι οποιοσδήποτε πολλαπλασιαμός με το 0 μας δίνει 0, ανεξάρτητα από την αριθμητική βάση.
3. Σε όλους τους πίνακες, η τρίτη γραμμή και η τρίτη στήλη ταυτίζονται με την πρώτη γραμμή και την πρώτη στήλη, αντίστοιχα. Αυτό, όπως είναι αναμενόμενο, οφείλεται στο ότι το 1 είναι το ουδέτερο στοιχείο του πολλαπλασιασμού, που με απλούστερα λόγια σημαίνει ότι όποιος αριθμός κι αν πολλαπλασιαστεί με το 1, παραμένει αναλλοίωτος. 
4. Σε όλους τους πίνακες, η τελευταία γραμμή και η τελευταία στήλη έχουν την ίδια μορφή: 0, 10, 20, ..., 100. Η ιδιότητα αυτή είναι επίσης αναμενόμενη αρκεί να αναλογιστεί κανείς ότι όποιος αριθμός n κι αν πολλαπλασιαστεί με την εκάστοτε βάση b=10, το αποτέλεσμα θα είναι \( n \times 10 = (n 0)_b \), όπως προκύπτει από το συνδυασμό του Θεωρήματος, του Ορισμού και της Παρατήρησης 1.
5. Όλοι οι πίνακες είναι συμμετρικοί ως προς τη κύρια διαγώνιο που ξεκινάει από την επάνω αριστερή γωνία και καταλήγει στην κάτω δεξιά γωνία. Αυτό είναι συνέπεια της αντιμεταθετικής ιδιότητας του πολλαπλασιασμού: \( k \times n = n \times k \).

Αν συγκρίνουμε τώρα την προπαίδεια στο δυαδικό με την προπαίδεια στο δεκαδικό σύστημα είναι ολοφάνερο ότι η πρώτη είναι κατά πολύ απλούστερη, αφού οι πράξεις που πρέπει να αποστηθίσουμε είναι μόνο 9, ενώ στη δεύτερη 121. Φανταστείτε λοιπόν έναν κόσμο στον οποίο οι άνθρωποι έχουν υιοθετήσει το δυαδικό αντί για το δεκαδικό σύστημα. Σε έναν τέτοιο κόσμο τα παιδιά θα ήταν 10 φορές πιο ευτυχισμένα...