Οι προπαίδειες

Από μικρή ηλικία μαθαίνουμε την προπαίδεια, τη «μία και μοναδική» προπαίδεια. Για την προπαίδεια έχουν γραφτεί χαριτωμένα παιδικά ποιηματάκια και τραγουδάκια, έχουν δημιουργηθεί όμορφες και εύπεπτες εικόνες, έχουν επινοηθεί έξυπνα τεχνάσματα που χρησιμοποιούν διάφορα μέσα, όπως για παράδειγμα τα δάχτυλα των χεριών, τεμνόμενες γραμμές, κτλ. Όλα αυτά με σκοπό να μάθουν τα παιδιά εύκολα και γρήγορα αυτό το πολύτιμο εργαλείο που θα τους επιτρέψει αργότερα να προχωρήσουν στα μαθηματικά. Ένα πράγμα όμως που άθελά μας παραβλέπουμε είναι ότι η προπαίδεια δεν είναι τελικά «μία και μοναδική». Απεναντίας, υπάρχουν τόσες προπαίδειες, όσοι είναι και οι φυσικοί αριθμοί, δηλαδή άπειρες! Το ότι μαθαίνουμε μόνο μία, οφείλεται αποκλειστικά στο γεγονός ότι εντελώς αυθαίρετα, το ανθρώπινο είδος, ανάμεσα από τα άπειρα αριθμητικά συστήματα, καθένα από τα οποία έχει ως βάση έναν φυσικό αριθμό, έχει επιλέξει να πορευτεί με το δεκαδικό σύστημα, το σύστημα δηλαδή που έχει ως βάση το δέκα.

Για τη διαδικασία εξαγωγής της προπαίδειας με οποιαδήποτε αριθμητική βάση είναι απαραίτητο το επόμενο Θεώρημα και ο επόμενος Ορισμός της Θεωρίας Αριθμών: 

Θεώρημα: Αν b είναι ένας φυσικός αριθμός μεγαλύτερος του 1, τότε κάθε φυσικός αριθμός n>0 έχει μια μονοσήμαντη παράσταση της μορφής 

\[n = n_0 + n_1 b + n_2 b^2 + \dots + n_m b^m\]

όπου \( n_m \ne 0 \) και \( 0 \le n_k < b \) για \( 0 \le k \le m \)

Ορισμός: Η έκφραση του αριθμού n στο b-δικό αριθμητικό σύστημα είναι:

\[n = (n_m n_{m-1} \dots n_1 n_0)_b\]

Για παράδειγμα ο αριθμος 24 στο 7-δικό σύστημα μεταφράζεται ως εξής: 

\[(24)_7 = 2 \times 7^1 + 4 \times 7^0=2 \times 7 + 4\]

όπως φαίνεται εύκολα αν στις σχέσεις του Θεωρήματος και του Ορισμού θέσουμε \(b=7, m=1, n_0=4, n_1=2\). Αξίζει να σημειωθεί ότι στο δεκαδικό σύστημα, χάριν απλότητας παραλείπεται η βάση, ώστε αντί για \( (n_m n_{m-1} \dots n_1 n_0)_{10} \) γράφουμε απλώς \( n_m n_{m-1} \dots n_1 n_0 \). Έτσι για παράδειγμα, αντί για \( (24)_{10} \) γράφουμε απλώς \( 24 \).

Έστω τώρα ότι θέλουμε να υπολογίσουμε το γινόμενο \( 3 \times 6 \) στο 7-δικό σύστημα. Ένας τρόπος να βρούμε το αποτέλεσμα είναι με αναγωγή στο 10-δικό σύστημα:  

\[ 3 \times 6 = 18 = 14 + 4 = 2 \times 7 + 4 = 2 \times 7^1 + 4 \times 7^0 = (24)_7 \]

Ένας πιο στοιχειώδης τρόπος, που είναι ανεξάρτητος από το 10-δικό σύστημα είναι ο εξής:

\[ 3 \times 6 = 6 + 6 + 6 = 6 + (1+5) + 6 = (6+1)+5+6=10+5+6= \]

\[ 10+5+(2+4) = 10+(5+2)+4=10+10+4=2 \times 10+4=20+4=24 \]

Άλλωστε, ακόμη κι αν ίσως δεν το έχουμε συνειδητοποιήσει, αυτός είναι ο τρόπος με τον οποίον γίνεται ο πολλαπλασιασμός και στο 10-δικό σύστημα.

Σε κάθε περίπτωση, βρίσκουμε ότι στο 7-δικό σύστημα \( 3 \times 6 = 24 \). Όσο αυθαίρετο κι αν φαίνεται αυτό το αποτέλεσμα, ας μην ξεχνάμε ότι είναι εξίσου αυθαίρετο με το γεγονός ότι \( 3 \times 6 = 18 \) στο 10-δικό σύστημα. Η «φυσικότητα» του τελευταίου έγκειται καθαρά και μόνο στην τεράστια εξοικείωση που έχουμε με το 10-δικό σύστημα.

Ακολουθώντας την παραπάνω λογική μπορούμε να συμπληρώσουμε την προπαίδεια για όποια βάση επιθυμούμε. Παρακάτω παρουσιάζονται οι προπαίδειες που αντιστοιχούν στα αριθμητικά συστήματα με βάση από το 1 ως το 10.

2-δικό σύστημα.

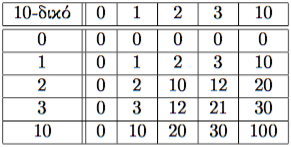
3-δικό σύστημα.

4-δικό σύστημα.

5-δικό σύστημα.

6-δικό σύστημα.

7-δικό σύστημα.

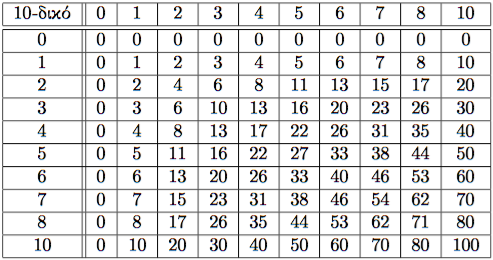
8-δικό σύστημα.

9-δικό σύστημα.

10-δικό σύστημα.

Φυσικά, όπως έχουμε ήδη αναφέρει, η λίστα δεν τελειώνει εδώ και θα μπορούσαμε να συνεχίσουμε με το 11-δικό, το 12-δικό κτλ. Η μόνη διαφορά με τα συστήματα που έχουν βάση μεγαλύτερη του 10 είναι ότι, σε σημειογραφικό επίπεδο, λόγω της εξάντλησης των δέκα γνωστών μας ψηφίων, πρέπει να επινοήσουμε καινούρια σύμβολα για το δέκα, το έντεκα, το δώδεκα, κ.ο.κ. Έτσι, για παράδειγμα, το 10 δεν μπορεί να έχει την έννοια του δέκα στο εντεκαδικό σύστημα, καθώς \( 10 = 1 \times 11 + 0 \), που με όρους δεκαδικού συστήματος είναι το 11. Για αυτό το λόγο, στο εντεκαδικό σύστημα, για το δέκα χρησιμοποιούμε κάποιο νέο σύμβολο, διαφορετικό από τα 0, 1, 2, ..., 9. Είθισται, ως δεξαμενή άντλησης νέων συμβόλων να χρησιμοποιείται το σύνολο των γραμμάτων του αλφαβήτου. Έτσι, για το 10 στο εντεκαδικό σύστημα, είναι βολικό να χρησιμοποιηθεί το «α», για το 11 στο δωδεκαδικό σύστημα το «β», κ.ο.κ. Ασφαλώς είναι φανερό ότι κάποια στιγμή εξαντλούνται τα γράμματα του αλφαβήτου. Στην περίπτωση αυτή είναι αναπόφευκτο να επινοηθούν νέα σύμβολα. Ωστόσο, συστήματα με τόσο μεγάλη βάση δεν έχουν καμία πρακτική αξία για εμάς. Ενδεικτικά, παρακάτω παρουσιάζεται και η προπαίδεια του 11-δικού συστήματος, όπου το δέκα συμβολίζεται με α.

11-δικό σύστημα.

Με βάση τους παραπάνω πίνακες, αξίζει να κάνουμε μερικές χρήσιμες παρατηρήσεις. 

1. Αρχικά, μπορεί εύκολα κανείς να καταλήξει στο εσφαλμένο συμπέρασμα ότι υπάρχει τυπογραφικό λάθος, καθώς σε όλους τους πίνακες γράφει επάνω αριστερά 10-δικό. Στην πραγματικότητα όμως δεν υπάρχει κανένα τυπογραφικό λάθος. Το μυστικό είναι ότι σε κάθε σύστημα η βάση εκφράζεται με το 10. Το κάθε σύστημα στην ουσία διαφέρει μόνο στο πλήθος των ψηφίων που χρησιμοποιεί.
2. Σε όλους τους πίνακες, η δεύτερη γραμμή και η δεύτερη στήλη περιέχει μόνο μηδενικά. Αυτό είναι ασφαλώς συνεπές με το ότι οποιοσδήποτε πολλαπλασιαμός με το 0 μας δίνει 0, ανεξάρτητα από την αριθμητική βάση.
3. Σε όλους τους πίνακες, η τρίτη γραμμή και η τρίτη στήλη ταυτίζονται με την πρώτη γραμμή και την πρώτη στήλη, αντίστοιχα. Αυτό, όπως είναι αναμενόμενο, οφείλεται στο ότι το 1 είναι το ουδέτερο στοιχείο του πολλαπλασιασμού, που με απλούστερα λόγια σημαίνει ότι όποιος αριθμός κι αν πολλαπλασιαστεί με το 1, παραμένει αναλλοίωτος. 
4. Σε όλους τους πίνακες, η τελευταία γραμμή και η τελευταία στήλη έχουν την ίδια μορφή: 0, 10, 20, ..., 100. Η ιδιότητα αυτή είναι επίσης αναμενόμενη αρκεί να αναλογιστεί κανείς ότι όποιος αριθμός n κι αν πολλαπλασιαστεί με την εκάστοτε βάση b=10, το αποτέλεσμα θα είναι \( n \times 10 = (n 0)_b \), όπως προκύπτει από το συνδυασμό του Θεωρήματος, του Ορισμού και της Παρατήρησης 1.
5. Όλοι οι πίνακες είναι συμμετρικοί ως προς τη κύρια διαγώνιο που ξεκινάει από την επάνω αριστερή γωνία και καταλήγει στην κάτω δεξιά γωνία. Αυτό είναι συνέπεια της αντιμεταθετικής ιδιότητας του πολλαπλασιασμού: \( k \times n = n \times k \).

Αν συγκρίνουμε τώρα την προπαίδεια στο δυαδικό με την προπαίδεια στο δεκαδικό σύστημα είναι ολοφάνερο ότι η πρώτη είναι κατά πολύ απλούστερη, αφού οι πράξεις που πρέπει να αποστηθίσουμε είναι μόνο 9, ενώ στη δεύτερη 121. Φανταστείτε λοιπόν έναν κόσμο στον οποίο οι άνθρωποι έχουν υιοθετήσει το δυαδικό αντί για το δεκαδικό σύστημα. Σε έναν τέτοιο κόσμο τα παιδιά θα ήταν 10 φορές πιο ευτυχισμένα...