Τα μαθηματικά του ΚΙΝΟ

Το ΚΙΝΟ είναι ένα «τυχερό παίγνιο» το οποίο δίνει την ελπίδα για μεγάλα κέρδη στους συμμετέχοντες. Οι κανόνες του είναι απλοί και αυτό σε συνδυασμό με τα πραγματικού χρόνου αποτελέσματα είναι δυο λόγοι για τους οποίους είναι ένα τόσο διαδεδομένο παιχνίδι. Όπως συμβαίνει συνήθως με αυτού του είδους τα παιχνίδια, αν και ανήκουν στην κατηγορία του τζόγου κι ενέχουν τον κίνδυνο του εθισμού, εντούτοις προσφέρουν πολύ ενδιαφέροντα μαθηματικά προβλήματα πιθανοτήτων. Το ίδιο συμβαίνει και με το ΚΙΝΟ. Πιο συγκεκριμένα, το ΚΙΝΟ σε κάθε διαγωνισμό κληρώνει 20 τυχαίους από τους 80 πρώτους φυσικούς αριθμούς και ζητάει από τους συμμετέχοντες να προβλέψουν τους περισσότερους δυνατούς από τους κληρωθέντες αριθμούς επιστρέφοντας σε περίπτωση επιτυχίας τα αντίστοιχα κέρδη. Ο κάθε παίκτης ορίζει πόσους αριθμούς επιδιώκει να προβλέψει από 1 έως 12 και ανάλογα με το πόσους από αυτούς προβλέπει σωστά, παίρνει και τις αντίστοιχες αποδόσεις. Κάποια εύλογα ερωτήματα λοιπόν που ανακύπτουν είναι τα εξής: Πόσο καλές είναι αυτές οι αποδόσεις; Ποια η πιθανότητα να κερδίσει κανείς; Είναι δίκαιο παιχνίδι το ΚΙΝΟ; Παρακάτω θα προσπαθήσουμε να απαντήσουμε αυτές τις ερωτήσεις με αυστηρά μαθηματικό τρόπο.

Υπάρχει ένα κριτήριο το οποίο αποφαίνεται εάν ένα τυχερό παιχνίδι είναι δίκαιο ή όχι. Για το κριτήριο αυτό είναι απαραίτητος ο συντελεστής μέσου αναμενόμενου κέρδους c, ο οποίος μας δείχνει τι ποσοστό του πονταρίσματος αναμένεται να επιστραφεί ως κέρδος στον παίκτη. Π.χ., εάν c=1.5 αυτό σημαίνει ότι αν κάποιος ποντάρει μια νομισματική μονάδα (π.χ., ευρώ), θα λάβει πίσω 1.5 μονάδες (ευρώ) και συνεπώς το κέρδος του θα είναι 0.5 μονάδες. Είναι φανερό ότι όταν c>1 ο παίκτης αναμένεται να βγει κερδισμένος από οποιοδήποτε ποντάρισμα, όταν c<1 αναμένεται να βγει χαμένος, ενώ όταν c=1 αναμένεται να πάρει απλά πίσω το ποντάρισμα. Φυσικά κάτι τέτοιο δε θα συμβαίνει κάθε φορά που κάποιος παίζει, ωστόσο ο νόμος των μεγάλων αριθμών εγγυάται ότι εάν η διαδικασία του πονταρίσματος επαναλαμβάνεται για πολλές φορές τότε το συνολικό κέρδος θα πλησιάζει την τιμή που καθορίζεται από τον συντελεστή c. Με βάση τα παραπάνω, είναι προφανές ότι ένα παιχνίδι για να χαρακτηριστεί δίκαιο θα πρέπει να έχει συντελεστή αναμενόμενου κέρδους c=1. Ας δούμε λοιπόν τι συμβαίνει με το c του ΚΙΝΟ.

Για την εύρεση του c, είναι απαραίτητο να υπολογιστούν οι πιθανότητες επιτυχίας όλων των δυνατών διαφορετικών περιπτώσεων που υπάρχουν σε μια κλήρωση. Με χρήση Συνδυαστικής, η πιθανότητα να διαλέξει κάποιος K από ένα σύνολο N αριθμών, από αυτούς τους N να κληρωθούν οι D αριθμοί και S από τους K να περιέχονται σε αυτούς τους D αριθμούς δίνεται από τον παρακάτω τύπο:

\[ P_K^S = \frac{\binom{D}{S} \binom{N-D}{K-S}}{\binom{N}{K}} \]

Στην περίπτωση του ΚΙΝΟ, το N=80 και το D=20. Οπότε στη μελέτη μας θα χρειαστεί να υπολογίσουμε τις πιθανότητες επιτυχίας για τις διάφορες δυνατές τιμές των μεταβλητών K και S. Οι πιθανότητες αυτές συνοψίζονται στον επόμενο πίνακα. 

Πίνακας 1. Πιθανότητες όλων των δυνατών ενδεχομένων.

Παραδείγματος χάριν, εφόσον το (2, 3)-στοιχείο του Πίνακα 1 είναι 0.14, αυτό σημαίνει ότι εάν επιλέξουμε 3 αριθμούς, τότε η πιθανότητα να κληρωθούν οι 2 από αυτούς ισούται με 14%. Οι παραπάνω πιθανότητες έχουν στρογγυλοποιηθεί στο δεύτερο δεκαδικό ψηφίο, ενώ όταν οι τιμές είναι μικρότερες του 0.01, αναγράφεται απλά η τάξη μεγέθους τους ως μια δύναμη του 10. 

Στο σημείο αυτό, προτού προχωρήσουμε παραπέρα, θα πρέπει να τονίσουμε ότι στην πραγματικότητα αναζητάμε 12 συντελεστές c, ένα για κάθε πλήθος επιλογών Κ από 1 μέχρι 12, μιας και το Κ καθορίζει κάθε φορά κι ένα διαφορετικό παιχνίδι. Για κάθε Κ λοιπόν, ο συντελεστής μέσου αναμενόμενου κέρδους c_K προκύπτει από τον τύπο:

\[ c_K = \sum_{(S,K) \in \mathcal{I}_K} odds(S,K) \,\, prob(S,K) \]

όπου I_K είναι το σύνολο όλων των αμοιβαίως αποκλειόμενων γεγονότων τα οποία καθορίζονται από τα ζεύγη (S, K) για τις διάφορες τιμές του S και για ένα συγκεκριμένο K, odds(S, K) είναι η πραγματική απόδοση που αφορά στο ζεύγος (S, K) και prob(S, K) είναι η πιθανότητα να συμβεί το ζεύγος (S, K). Στην προκειμένη περίπτωση σταθεροποιώντας το Κ σε μια από τις τιμές από 1 έως 12, το S παίρνει τις ακέραιες τιμές 0, 1,..., 12 και το αντίστοιχο γεγονός υπενθυμίζουμε ότι σημαίνει S επιτυχίες στις K επιλογές. 

Είναι φανερό ότι για να υπολογίσουμε τα c_K, χρειαζόμαστε τις πραγματικές αποδόσεις για κάθε γεγονός. Οι αποδόσεις αυτές συγκεντρώνονται στον Πίνακα 2.  

Πίνακας 2. Πραγματικές αποδόσεις.

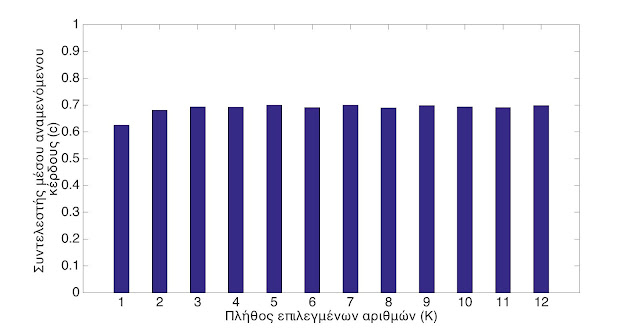
Οι τιμές των c_K για κάθε ξεχωριστό K που υπολογίζονται με βάση τον προηγούμενο τύπο συνοψίζονται στο Διάγραμμα 1.

Διάγραμμα 1. Συντελεστής μέσου αναμενόμενου κέρδους c_K για τις διάφορες τιμές του K.

Από το Διάγραμμα 1 παρατηρούμε ότι σχεδόν για οποιονδήποτε αριθμό επιλογών K, ο συντελεστής μέσου αναμενόμενου κέρδους είναι περίπου ίσος με 0.7. Αυτό δείχνει ότι σε κάθε περίπτωση ο παίκτης αναμένεται να πάρει πίσω το 70% ή ισοδύναμα να χάσει το 30% των χρημάτων που ποντάρισε, ποσοστό που αποτελεί τη λεγόμενη γκανιότα. Το γενικό συμπέρασμα λοιπόν που απαντά και στις ερωτήσεις που τέθηκαν στην αρχή είναι ότι το ΚΙΝΟ, από μαθηματική άποψη δεν είναι ένα δίκαιο παιχνίδι καθώς οι αποδόσεις είναι μικρότερες αυτών που θα έπρεπε και συνεπώς εάν κάποιος παίζει ΚΙΝΟ θα πρέπει να έχει υπόψιν του ότι αν και υπάρχει ασφαλώς η πιθανότητα να κερδίσει και μάλιστα πολλά λεφτά, ωστόσο είναι μεγαλύτερη η πιθανότητα να βγει χαμένος.